Nelle lezioni precedenti abbiamo visto come è possibile applicare il TEOREMA DI PITAGORA per trovare la misura dell’ipotenusa di un triangolo rettangolo conoscendo la misura dei suoi cateti.. Ora vogliamo vedere come è possibile trovare la misura di un cateto del triangolo rettangolo se conosciamo la misura dell’altro cateto e quella dell’ipotenusa.. Condividi. Due schemi riassuntivi e molto intuitivi per capire il Teorema di Pitagora. Gli schemi sono simili, ma variano leggermente a seconda di come potrà essere impostato il problema oggetto di studio. Sono presenti: la formula generale e tutta una serie di formule dirette ed inverse.

Teorema di Pitagora 2 YouTube

TEOREMA DI PITAGORA POLIGONI Blog di infoscholastic

tavola numericaa Matematica scuola media, Attività di matematica, Teorema di pitagora
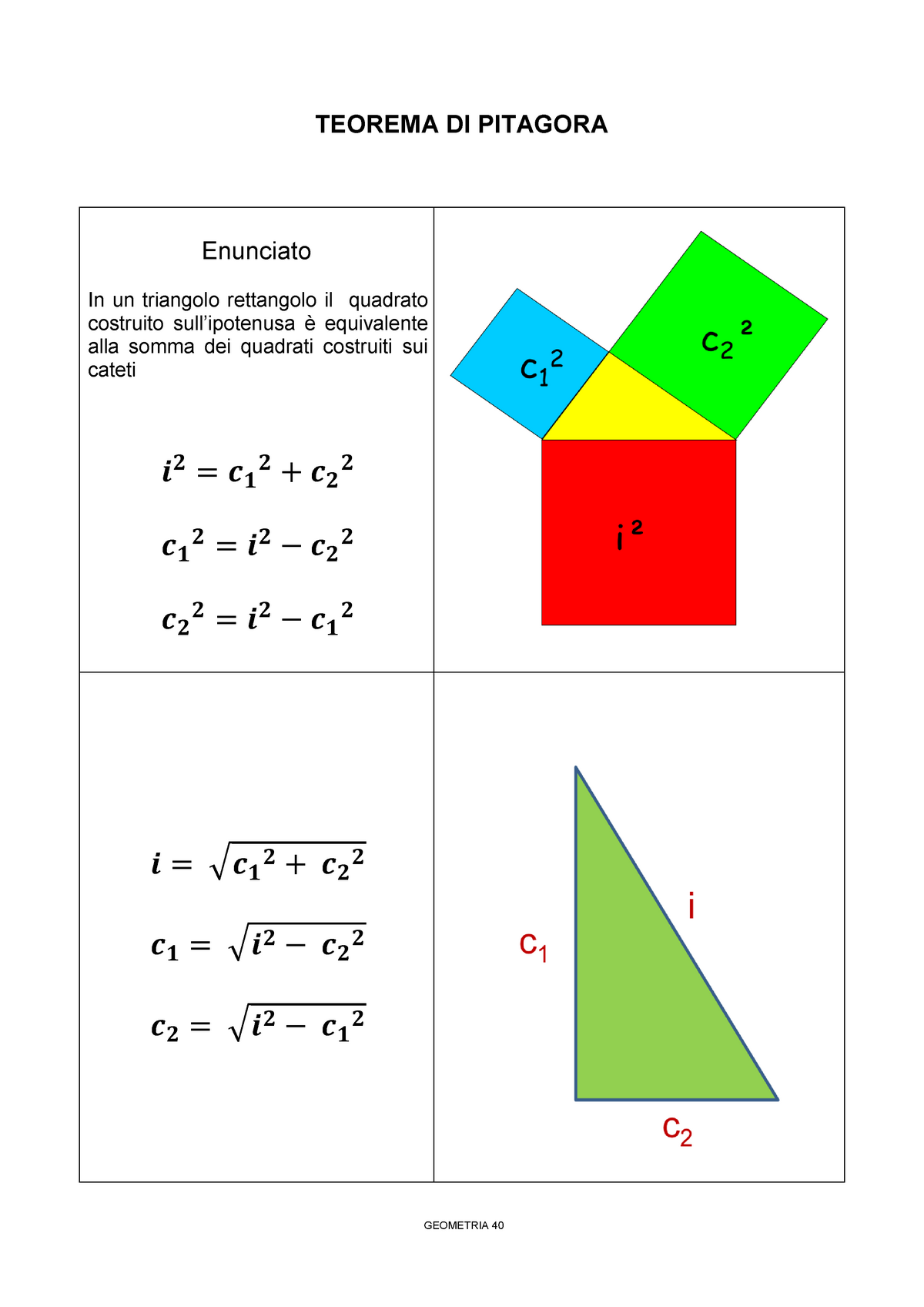
Teorema di Pitagora appunti lezioni fisica con elementi di matematica TEOREMA DI PITAGORA

Teorema di Pitagora in breve YouTube
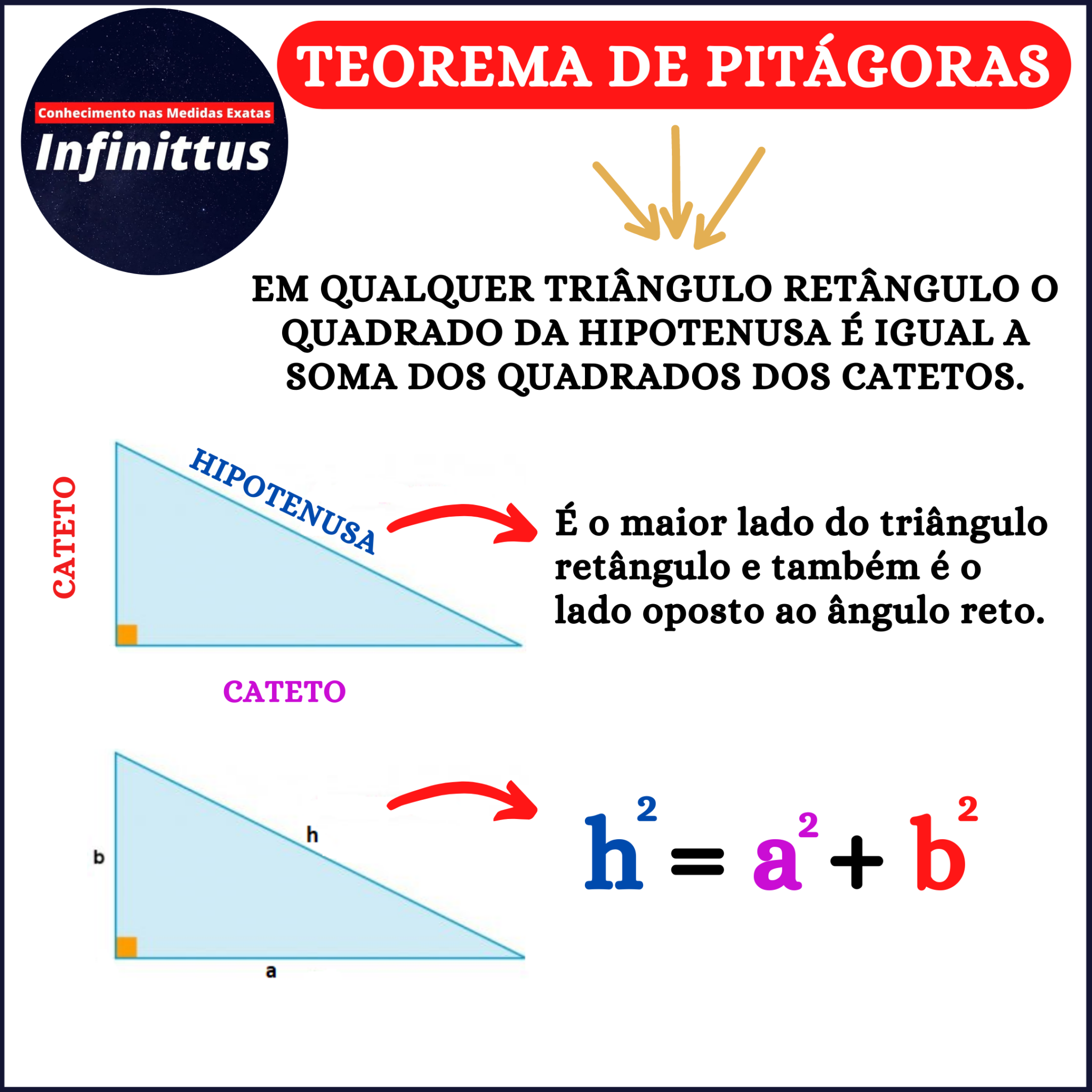
Você lembra qual é a fórmula e o conceito do Teorema de Pitágoras?

TEOREMA DI PITAGORA YouTube

Il Teorema Di Pitagora 2ª Media Teorema di pitagora, Matematica scuola
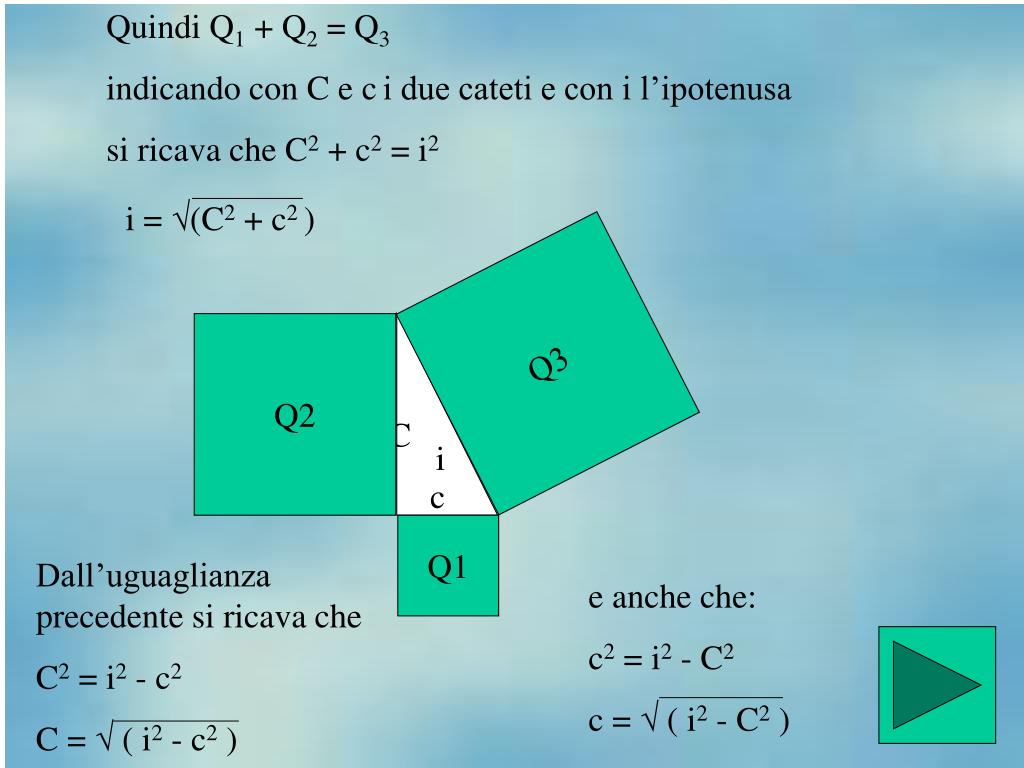
PPT TEOREMA DI PITAGORA PowerPoint Presentation, free download ID5264201

Teorema Di Pitagora

Teorema di Pitagora YouTube

Calaméo IL TEOREMA DI PITAGORA

Teorema di Pitagora YouTube
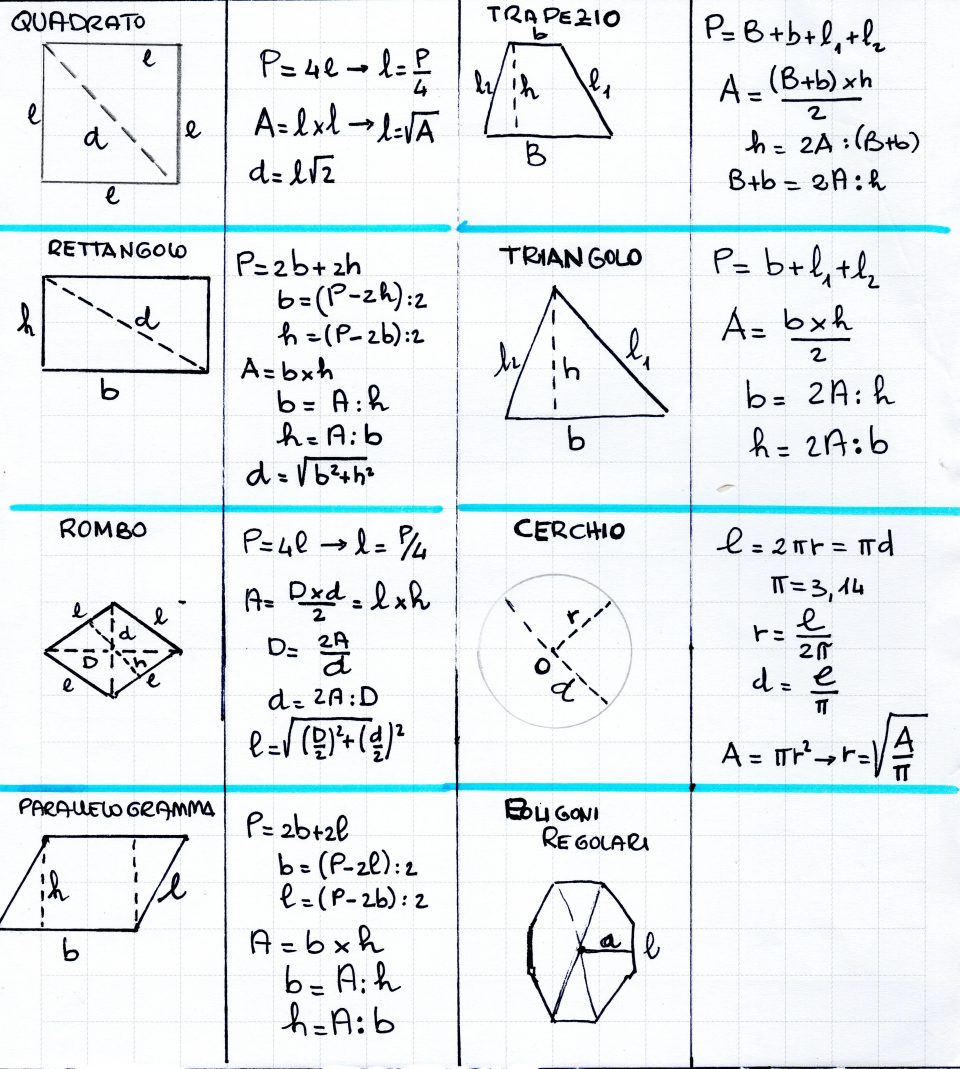
RIPASSIAMO IL TEOREMA DI PITAGORA lezioniignoranti

teoremadipitagora.jpg 642×1.311 pixel Teorema di pitagora, Matematica scuola media, Istruzione
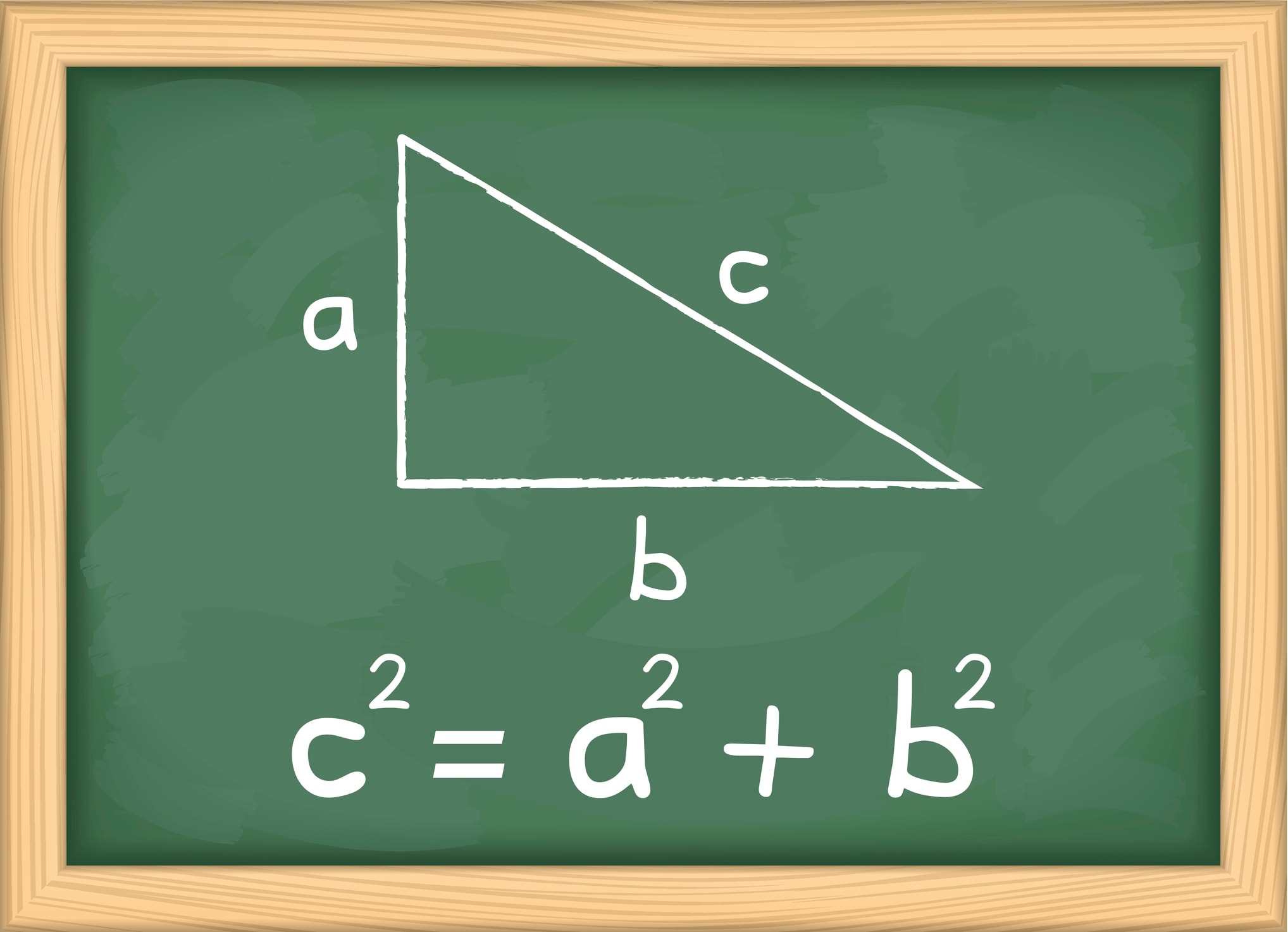
Teorema di Pitagora spiegazione ed esercizi Studenti.it
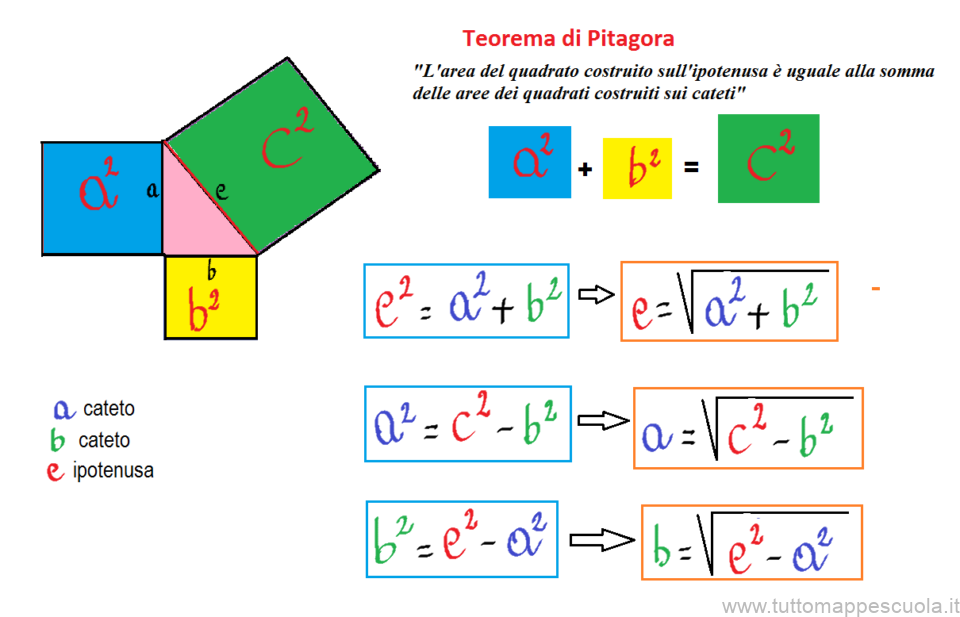
Teorema di Pitagora Tutto Mappe Scuola

Problemi Teorema di Pitagora Mauitaui e la matematica

RIPASSIAMO IL TEOREMA DI PITAGORA lezioniignoranti
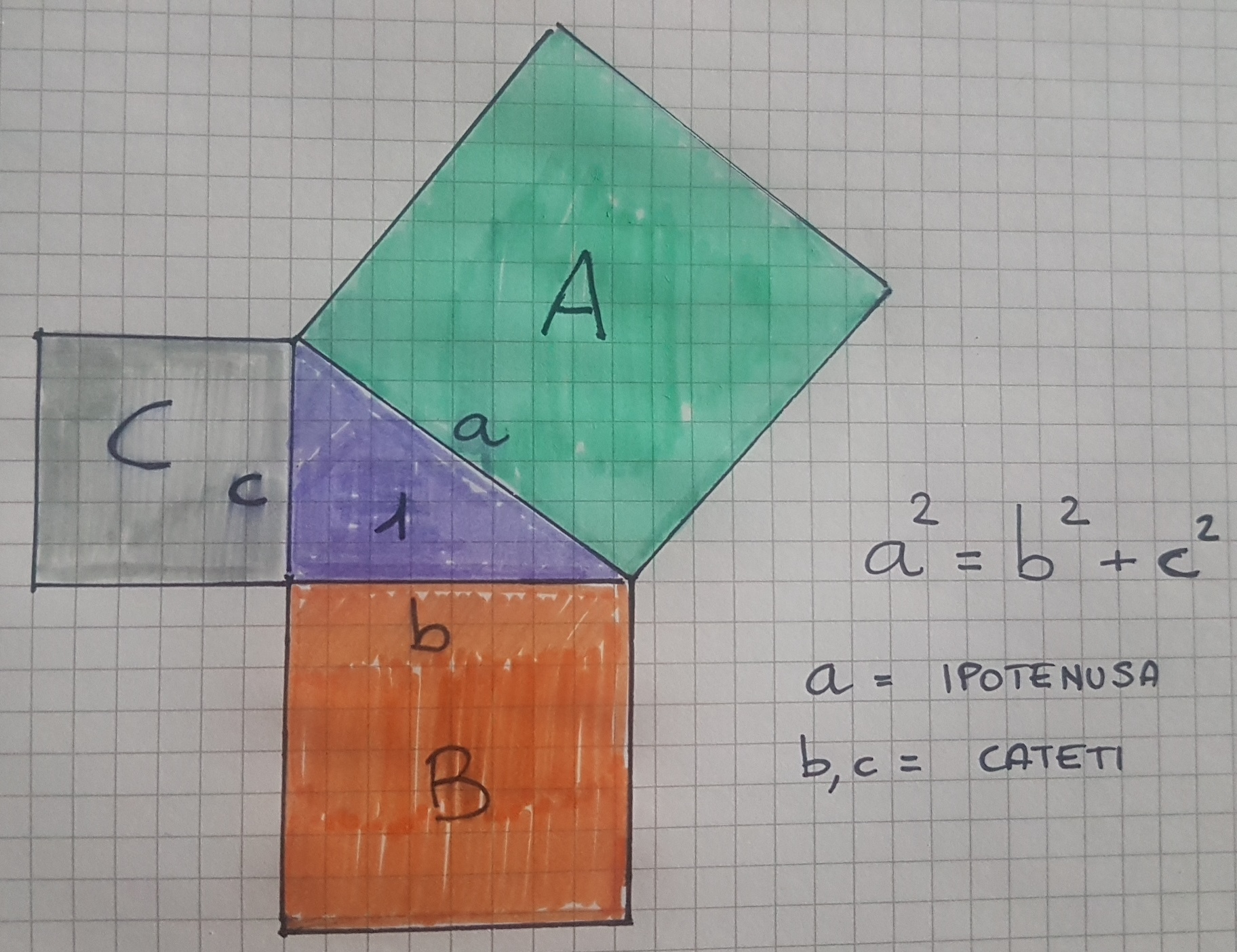
TEOREMA DI PITAGORA lezioniignoranti
AQ1 = i2. Il QUADRATO COSTRUITO SUL CATETO 1, che abbiamo chiamato Q3 , ha come lato il cateto c1 , quindi la sua area. AQ3 = c12. Infine il QUADRATO COSTRUITO SUL CATETOc2, che abbiamo chiamato Q2 , ha come lato il cateto c2 , quindi la sua area sarà data da: AQ2 = c22. Ora, sostituendo a. le rispettive aree possiamo scrivere: i2 = c12 + c22.. un cateto conoscendo la misura dell’ altro cateto , dell’ ipotenusa e dell’ altezza relativa all’ipotenusa. Dalla formula precedente possiamo ricavare le seguenti formule inverse: i = (c1 x c2)/ h. c1 = (i xh)/ c2. c2 = (i xh)/ c1. Lezione precedente – Lezione successiva. Indice degli argomenti sul teorema di Pitagora.


